Introducción
Imagina tener un número y querer saber cuáles son sus «ingredientes» básicos, como si fuera una receta. En matemáticas, estos «ingredientes» son los números primos, y el proceso de encontrarlos se llama factorización en factores primos.
¿Qué es un número primo?
Un número primo es aquel que solo es divisible por 1 y por sí mismo. Por ejemplo, 2, 3, 5, 7, 11 son números primos.
¿Por qué es importante la factorización en factores primos?
La factorización en factores primos tiene muchas aplicaciones en matemáticas, como:
- Simplificar fracciones.
- Encontrar el mínimo común múltiplo (m.c.m.) y el máximo común divisor (m.c.d.) de dos o más números.
- Resolver ecuaciones.
- Y muchas más…
¿Cómo factorizar un número en factores primos?
- Escoge un número: Comenzamos con cualquier número compuesto (es decir, que no sea primo).
- Encuentra un divisor primo: Busca el número primo más pequeño que divida al número original.
- Divide y repite: Divide el número original entre el divisor primo y anota el resultado. Repite este proceso con el resultado obtenido hasta que solo te queden números primos.
Ejemplo: Factoricemos el número 36.
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
Entonces, la factorización en factores primos de 36 es: 2 × 2 × 3 × 3, o lo que es lo mismo, 2² × 3².
El árbol de factores
Una forma visual de representar la factorización en factores primos es a través de un árbol de factores.
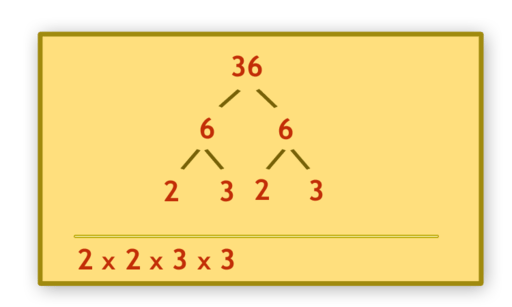
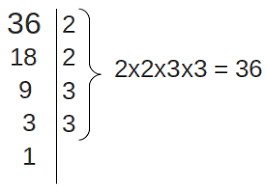
Aplicaciones de la factorización en factores primos
- Simplificación de fracciones: Al factorizar el numerador y el denominador de una fracción, podemos identificar los factores comunes y simplificarlos.
- M.C.M. y m.c.d.: El m.c.m. es el menor múltiplo común de dos o más números, y el m.c.d. es el mayor divisor común de dos o más números. La factorización en factores primos nos ayuda a calcularlos de manera eficiente.
Ejercicios
- Factoriza los siguientes números en factores primos: 24, 60, 105.
- Encuentra el m.c.m. y el m.c.d. de 12 y 18.
Conclusión
La factorización en factores primos es una herramienta fundamental en matemáticas que nos permite descomponer los números en sus elementos básicos. Al comprender este concepto, podemos resolver una gran variedad de problemas y profundizar en el estudio de las matemáticas.
